Нахождение функции, описывающей собственные колебания мембраны

Материалы о физике / Собственные колебания пластин / Нахождение функции, описывающей собственные колебания мембраны

Страница 5

Собственные колебания круглой мембраны

Сравним теперь результаты решения двух задач о нахождении функции, характеризующей прогиб мембраны, также при заданных различных граничных условиях, одинаковых начальных условиях, но уже для круглой мембраны.

(2.3.1)

Уравнение колебаний круглой мембраны в полярных координатах имеет вид

png">.

Будем искать решение этого уравнения при заданных начальных условиях

(2.3.2)

(2.3.3)

и граничных условиях

.

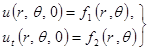
Применим метод разделения переменных. Пусть

.

Подставляем полученное выражение для функции в уравнение (2.3.1), получаем:

.

(2.3.4)

Так как нужно найти нетривиальное решение задачи, то

, полученное равенство можно поделить на

. Тогда

.

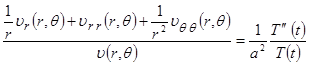Из соотношения (2.3.4) получаем однородное дифференциальное уравнение второго порядка для функции

,

(2.3.5)

решением, которого будет функция (см. 2.2)

,

и следующую задачу на собственные значения для функции :

(2.3.6)

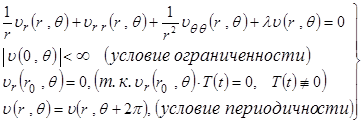
К задаче (2.3.6) снова применим метод Фурье для нахождения функции . Пусть , подставляем в уравнение для функции .

Поделим данное равенство на :

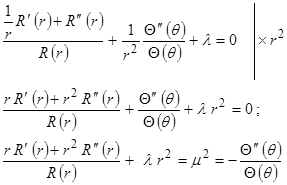
Так как левая часть соотношения () функция только переменной r, а правая () - только переменной , то равенство должно сохранять постоянное значение, пусть оно равно . При данном предположении получаем:

1) однородное дифференциальное уравнение второго порядка для нахождения функции :

Страницы: 1 2 3 4 5 6 7 8