Особенности расчета и проектирования

Степень возрастания сопротивления с температурой у заготовок диаметром 12 и 35 мм также подтверждает влияние скинн-эффекта.

В то время как сопротивление заготовки диаметром 35 мм, у которой скинн-эффект более резко выражен (отношение R2/δ2 большое), возрастает всего в 2 раза, у заготовки диаметром 12 мм (R2/δ2 меньше) оно возрастает уже в 4,5 раза.

Сопротивления указанных заготовок, вычисленные по формуле (34) с учетом изменения электрического сопротивления и магнитной проницаемости от температуры (μ = 200 при t = 200-760° С и μ = 1 при t = 760° С), несколько больше экспериментальных. Это, провидимому, объясняется тем, что абсолютное значение магнитной проницаемости и характер зависимости ее от температуры взяты отличными от расчетных.

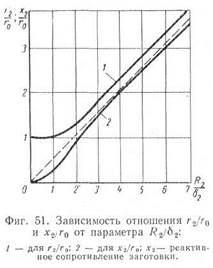
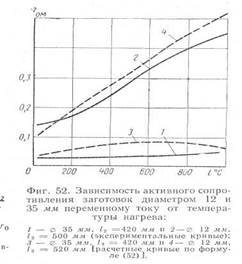
Рисунок 5.6 – График Рисунок 5.7 - График

Следовательно, скинн-эффект при низких температурах существенно сказывается на активном сопротивлении.

Необходимо также считаться и с реактивным сопротивлением детали.

Реактивное сопротивление определяется по формуле, аналогичной формуле (34).

Если графически выразить зависимость реактивного сопротивления от отношения R2/δ2, то получится кривая 2, изображенная на рисунке 5.6.

Модуль общего сопротивления нагреваемой детали определяется по известной формуле: (35)

При равенстве активного и реактивного сопротивлений полное сопротивление детали равно:

r2 = 1,4r2 = 1,41Х2.

Приведенные выше формулы и графики справедливы для цилиндрических деталей. В общем случае для любого сечения, например для сечения прямоугольной формы, можно воспользоваться формулами, рекомендуемыми проф. Л. Р. Нейманом.

Активное сопротивление детали:

. (36)

Реактивное сопротивление:

. (37)

Полное сопротивление:

(38)

где l2 — длина нагреваемой детали в см;

и2 — периметр поперечного сечения детали в см;

μ — магнитная проницаемость материала;

ς2 —удельное электрическое сопротивление в .ом-см;

f — частота тока.

Из всех переменных, входящих в формулы (36)—(38), неизвестной является магнитная проницаемость. Так как она определяется неоднозначно в зависимости от напряжения магнитного поля (тока) и гистерезиса, а последние зависят еще и от температуры, то найти ее весьма затруднительно.

Поэтому для расчета сопротивления заготовок, находящихся в холодном состоянии, следует брать определенное значение магнитной проницаемости для данной стали и считать ее постоянной до температуры 750—780 °С, а свыше этой температуры — равной единице.

Определение напряжения на нагреваемой детали

Напряжение на нагреваемой детали необходимо знать для определения вторичного напряжения силового трансформатора, так как без этого нельзя рассчитать число витков обмоток последнего.

Напряжение, потребное на заготовке для нагрева ее до заданной температуры, определяется по формуле: (39)

где z2 — определяется по формуле (38);

P2— определяется по формуле (29);

r2 — определяется по формуле (36).

В случае, когда скинн-эффектом можно пренебречь (при температуре нагрева выше точки Кюри для заготовок диаметром до 70 мм), формулу (39) можно выразить через параметры детали и теплоемкость:

. (40)