Относительное движение материальной точки

где Х – общее решение соответствующего однородного уравнения,

-частное решение неоднородного уравнения.

Однородное уравнение имеет вид

=0, (1.1.4)

которому соответствует следующее характеристическое уравнение

png">

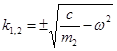i,

Т.к. величина под корнем отрицательна, то общим решением однородного дифференциального уравнения (1.1.3) будет являться функция:

Х=,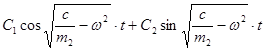

где С1 и С2 – постоянные интегрирования.

Частное решение уравнения (1.1.3) будем находить как результат суперпозиции двух решений: .

Для имеем:

(1.1.5)

, где k=0, значит

Подставим в (1.1.4):

При sin:

B=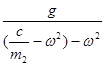

При cos:

A=

Тогда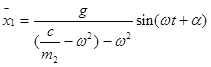

Для имеем:

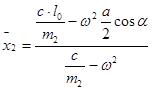
Тогда общее решение дифференциального уравнения относительного движения шарика (1.1.3) принимает вид

x=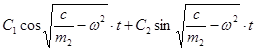

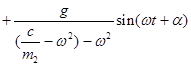
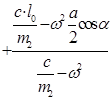
Скорость этого движения равна

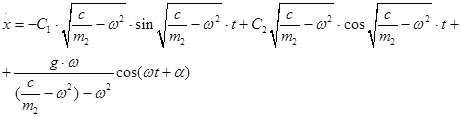
Составляющую реакции стенки трубки Ny определим из второго уравнения системы (1.1.2)

где определяется соответствующим выражением.