Определение реакций опор составной конструкции (система двух тел)
Дано :
R2=15; r2=10; R3=20; r3=20
X=C2t2+C1t+C0
При t=0 x0=8 ![]() =4
=4
t2=2 x2=44 см
X0=2C2t+C1
C0=8
C1=4
44=C2 *22+4*2+8
4C2=44-8-8=28
C2=7
X=7t2+4t+8
![]() =V=14t+4
=V=14t+4
a=![]() =14
=14
V=r2![]() 2
2
R2
png">2=R3
![]() 3
3
![]() 3=V*R2/(r2*R3)=(14t+4)*15/10*20=1,05t+0,3
3=V*R2/(r2*R3)=(14t+4)*15/10*20=1,05t+0,3
![]() 3=
3=![]() 3=1,05
3=1,05
Vm=r3*![]() 3=20*(1,05t+0,3)=21t+6
3=20*(1,05t+0,3)=21t+6
atm=r3![]()
![]() =1,05t
=1,05t
atm=R3![]() =20*1,05t=21t
=20*1,05t=21t
anm=R3![]() 23=20*(1,05t+0,3)2=20*(1,05(t+0,28)2
23=20*(1,05t+0,3)2=20*(1,05(t+0,28)2
a=![]()
5. Применение теоремы об изменении кинетической энергии к изучению движения механической системы
Исходные данные.
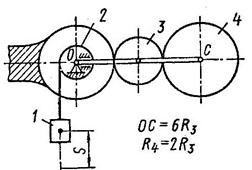
Механическая система под действием сил тяжести приходит в движение из состояния покоя. Трение скольжения тела 1 и сопротивление качению тела 3 отсутствует. Массой водила пренебречь.
Массы тел - m1, m2, m3, m4; R2, R3, R4 – радиусы окружностей.
|
m1, кг |
m2, кг |
m3, кг |
m4, кг |
R2, см |
R3, см |
s, м |
|
m |
m/10 |
m/20 |
m/10 |
10 |
12 |
0.05π |
Найти.
Пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определит скорость тела 1 в тот момент, когда пройденный им путь станет равным s.
Решение.
1. Применим к механической системе теорему об изменении кинетической энергии.
![]() ,
,
где T0 и T – кинетическая энергия системы в начальном и конечном положениях; ![]() – сумма работ внешних сил, приложенных к системе, на перемещении из начального положения в конечное;
– сумма работ внешних сил, приложенных к системе, на перемещении из начального положения в конечное; ![]() - сумма работ внутренних сил системы на том же перемещении.
- сумма работ внутренних сил системы на том же перемещении.
Для рассматриваемых систем, состоящих из абсолютно твёрдых тел, соединённых нерастяжимыми нитями и стержнями ![]() . Так как в начальном положении система находится в покое, то T0=0.
. Так как в начальном положении система находится в покое, то T0=0.
Следовательно, уравнение (1) принимает вид:
![]() .
.
2. Определим угол, на который повернётся водило, когда груз 1 пройдёт расстояние s.
![]() .
.
То есть когда груз 1 пройдёт путь s, система повернётся на угол 90º.
3. Вычислим кинетическую энергию системы в конечном положении как сумму кинетических энергий тел 1, 2, 3, 4.
T = T1 + T2 + T3 + T4.
а) Кинетическая энергия груза 1, движущегося поступательно равна:
![]() .
.
б) Кинетическая энергия катка 2, вращающегося вокруг своей оси равна:
![]() ,
,
где ![]() - момент инерции катка 2,
- момент инерции катка 2, ![]() - угловая скорость катка 2.
- угловая скорость катка 2.
Отсюда получаем, что
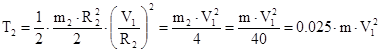 .
.
в) Кинетическая энергия катка 3, совершающего плоско-параллельное движение, равна:
![]() ,
,
где ![]() - скорость центра масс катка 3,
- скорость центра масс катка 3,
![]() -угловая скорость мгновенного центра скоростей катка 3
-угловая скорость мгновенного центра скоростей катка 3
![]()
момент инерции катка 3 относительно мгновенного центра скоростей.
Отсюда получаем, что
![]()
г) Кинетическая энергия катка 4, совершающего плоскопараллельное движение, равна:
