Определение коэффициентов теплоотдачи
2.2.1 Аналитическое определение А1, А2, А12
Для определения коэффициентов теплоотдачи рассмотрим упрощенную эквивалентную тепловую схему замещения асинхронного двигателя закрытого исполнения [4,9], (см. рисунок 1.3). Коэффициенты теплоотдачи считаем постоянными, то есть одинаковыми в переходном и установившемся режимах. Следовательно, для их определения можно рассматривать схему (см. рисунок. 1.3) в установившемся режиме (рисунок 2.2), что значительно упрощает решение. Так же введем допущение, что двигатель имеет независимое принудительное охлаждение, то есть коэффициенты теплоотдачи одинаковы при выключенном и включенном двигателе.
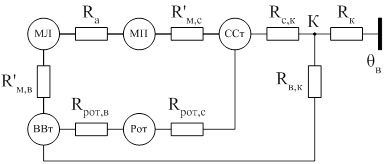
Рисунок 2.2 – Приведенная ЭТС закрытого обдуваемого двигателя для стационарного режима
Система уравнений для этой схемы имеет вид [2]:
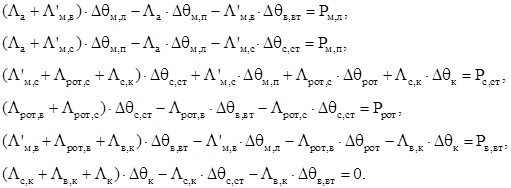 (2.2)
(2.2)
Так как в схеме (рисунок 2.2) рассмотрены лобовая и пазовая части обмотки в отдельности, а необходимо знать среднюю температуру обмотки, то по правилам эквивалентных преобразований [4], объединим эти источники в один (рисунок 2.3).
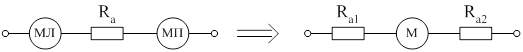
Рисунок 2.3 – Объединение лобовой и пазовой частей обмотки
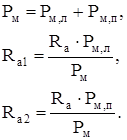
После преобразования (2.3) схема имеет 5 узлов (рисунок 2.4), то есть схеме соответствует система уравнений 5-го порядка.
Объединим сопротивления Ra1 с R'м,в и Ra2 с R'м,с:
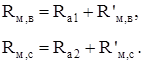 (2.4)
(2.4)
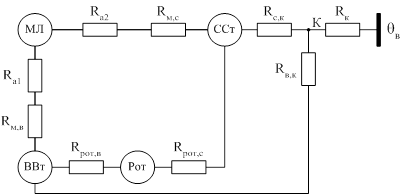
Рисунок 2.4 – ЭТС закрытого обдуваемого двигателя с объединенными пазовой и лобовой частями обмотки
В итоге имеем схему, изображенную на рисунке 2.5 которой соответствует система уравнений (2.5).
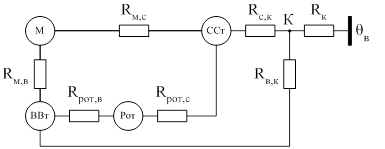
Рисунок 2.5 – Окончательный вид преобразованной ЭТС закрытого обдуваемого двигателя
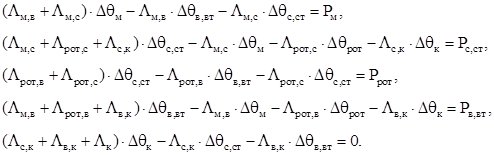 (2.5)
(2.5)
Систему уравнений (2.5) необходимо свести к системе уравнений второго порядка, в которой неизвестными выступили бы Δθм и Δθс,ст. Для сокращения записи выражений введем замену:
|
|
|
|
|
|
| |
|
|
|
(2.6) |
|
|
| |
|
|
|
Подставив в (2.5) выражения (2.6), получим:
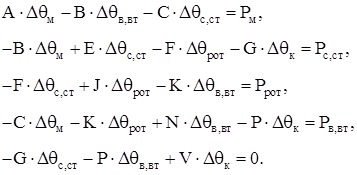 (2.7)
(2.7)
Пренебрежем механическими и добавочными потерями (Pв,вт=0), так как их величина мала по сравнению с основными потерями (потери в меди, стали, роторе) и, как следствие, они незначительно влияют на превышение температуры меди и стали.
Для того чтобы понизить порядок системы (2.7) выразим из последних трех уравнений Δθрот, Δθв,вт и Δθк через Δθм и Δθс,ст:
![]()
![]() ; (2.8)
; (2.8)
![]()
![]() ; (2.9)
; (2.9)
![]()
![]() . (2.10)
. (2.10)
Подставив выражение (2.9) в первое уравнение системы (2.7) получим:
