Обзор методов теплового расчета и существующих моделей
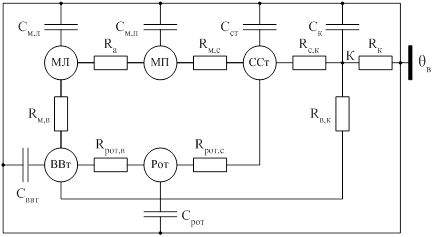
Рисунок 1.3 – Приведенная эквивалентная тепловая схема закрытого обдуваемого двигателя
Данная схема имеет шесть узлов: МЛ – лобовая часть обмотки, МП – пазовая часть обмотки, ВВт – воздух внутри машины, Рот – ротор, ССт – сталь сердечника статора, К – корпус двигателя (станина и подшипниковые щиты). Система уравнений нестационарного режима для схемы (см. рисунок 1.3) имеет вид [4,9]:
png">
где Δθм,л – превышение температуры лобовых частей обмотки;
Δθм,п – превышение температуры пазовой части обмотки;
Δθс,ст – превышение температуры стали пакета статора;
Δθрот – превышение температуры ротора;
Δθв,вт – превышение температуры воздуха внутри машины;
Δθк – превышение температуры корпуса;
См,л – теплоемкость лобовых частей обмотки;
См,п – теплоемкость пазовой части обмотки;
Сс,ст – теплоемкость стали пакета статора;
Срот – теплоемкость ротора;
Св,вт – теплоемкость воздуха внутри машины;
Ск – теплоемкость корпуса;
Рм,л – мощность электрических потерь в лобовых частях обмотки;
Рм,п – мощность электрических потерь в пазовой части обмотки;
Рс,ст – мощность потерь в стали статора на вихревые токи и гистерезис;
Ррот – мощность электрических потерь в роторе;
Рв,вт – мощность механических и добавочных потерь;
Λа – тепловая проводимость между лобовой и пазовой частями обмотки;
Λм,с – тепловая проводимость между пазовой частью обмотки и сердечником статора;
Λм,в-тепловая проводимость между лобовыми частями обмотки и воздухом внутри машины;
Λрот,в-тепловая проводимость между ротором и внутренним воздухом; Λрот,с – тепловая проводимость между ротором и сердечником статора; Λв,к – тепловая проводимость между воздухом внутри машины и корпусом;
Λс,к – тепловая проводимость между сердечником статора и корпусом;
Λк – тепловая проводимость между корпусом и внешним воздухом.
Системы дифференциальных уравнений (1.18) и (1.19), описывающие процессы нагрева двигателя, по сути, являются тепловыми моделями асинхронного двигателя. Основные факторы, определяющие точность расчета по уравнениям (1.18) и (1.19) следующие:
– точность задания источников теплоты, то есть потерь;
– точность определения тепловых проводимостей Λ, которые в свою очередь зависят:
а) от коэффициентов теплопроводности λ, которые подвержены значительному разбросу по технологическим причинам, под влиянием появления воздушных промежутков и т.п.;
б) от коэффициентов теплоотдачи α, поскольку имеющиеся для их определения эмпирические формулы и графики не могут учесть всех влияющих факторов и условий.
В связи с этим, а так же для сокращения объема вычислений, рядом авторов [7,8,9,10,11,12] предложены упрощенные математические модели нагрева асинхронного двигателя.
Так в [7,8] предложена тепловая модель двигателя, состоящая из двух цилиндров (рисунок 1.4).
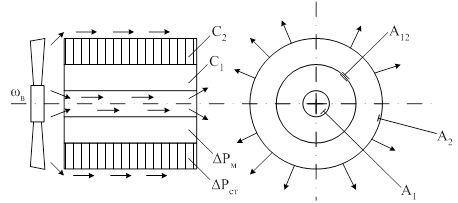
Рисунок 1.4 – Упрощенная модель двигателя как тела нагрева
Внешний цилиндр с теплоемкостью С2 моделирует массу железа машины, внутренний с теплоемкостью С1 – обмотки статора. Мощность теплового потока от стали к окружающей среде пропорциональна коэффициенту А2. Во внутреннем цилиндре предусмотрен канал, моделирующий отвод теплоты потоками воздуха от внутренних частей машины. Мощность теплового потока от меди статора к окружающей среде пропорциональна коэффициенту А1. Теплопередача между медью и сталью определяется коэффициентом А12, моделирующим термическое сопротивление изоляции.
Данной модели соответствует система уравнений [7,8]:
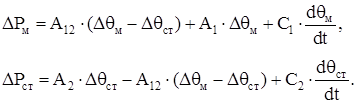 (1.20)
(1.20)
где Δθм и Δθст – превышения температуры меди и стали соответственно над температурой окружающего воздуха.
В [9] авторы получают уравнения, описывающие поведение температуры обмотки двигателя, путем аналитического решения системы (1.19)
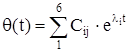 , (1.21)
, (1.21)
и замены решения (1.21), состоящего из шести экспонент, приближенным решением, состоящим из двух экспонент:
![]() , (1.22)
, (1.22)
где θ(t) – текущее превышение температуры обмотки;
θуст – превышение температуры в установившемся режиме;
