Модель келдыша – файсала – риса

В предположении, что лазерное поле является монохроматическим, т.е. напряженность поля лазерного излучения имеет вид

,

Келдыш получил вероятность ионизации в единицу времени. Без учета предэкспоненты для случая поля линейной поляризации эта экспоненциально малая вероятность не зависит от вида атомарного потенциала и имеет универсальный вид:

png"> , (15)

В полученном выражении введен так называемый параметр адиабатичности (или параметр Келдыша)

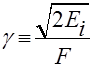; (16)

Именно он и определяет характер процесса нелинейной ионизации. Еще раз подчеркнем, что полученное выражение справедливо с потенциальной точностью. Для поля циркулярной или эллиптической поляризации аналогичное выражение выглядит более громоздко, и мы его не приводим.

Отметим также, что модель Келдыша калибровочно неинвариантна. Это означает, что выражение для вероятности нелинейной ионизации зависит от того, в какой форме выбирается взаимодействие атома с полем лазерного излучения: в калибровке « длины» или же в калибровке «скорости». Априори неясно, какая из этих форм дает более точные результаты [1].

3.2.1 Туннельный предел

Туннельный режим соответствует низкочастотному пределу, когда параметр адиабатичности много меньше единицы, точнее, . В этом пределе зависимость вероятности ионизации от частоты поля исчезает, а сама вероятность ионизации в единицу времени (15) приобретает ту же форму, что и для ионизации атома медленно меняющимся со временем электрическим полем, усредненную по периоду поля:

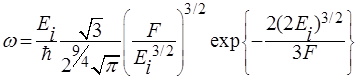, (17)

Основной вклад в эту вероятность дают слагаемые в сумме (15) с очень большими числами N поглощенных фотонов порядка . Эти числа велики по сравнению с минимальным числом поглощенных фотонов, допустимым законом сохранения энергии. Сумма по числам поглощенных фотонов в окрестности этого значения заменяется непрерывным интегрированием. Так выглядит надпороговое поглощение фотонов электромагнитного излучения в туннельном режиме ионизации [1].

Однако точное решение указанной задачи для ионизации основного состояния атома водорода постоянным электрическим полем с учетом усреднения вероятности по периоду медленно меняющегося поля линейной поляризации дает результат с другой предэкспонентой:

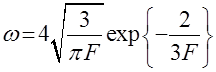; (18)

Необходимо отметить, что выражение (18) показывает вероятность ионизации одного атома в единицу времени [2].