Автоматизация расчетов параметров тепловой модели асинхронного двигателя

Расчеты коэффициентов системы дифференциальных уравнений (1.20) приведенные в разделах 3 – 6, для автоматизации вычислений реализованы с помощью системы MatLab.

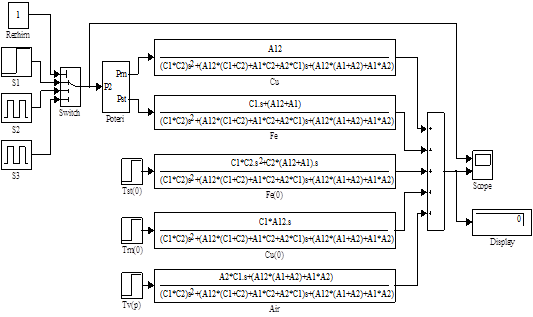
Рисунок 3.9 – Схема модели определения температуры стали

Эта система позволяет обрабатывать заранее подготовленную последовательность команд и операторов, записанную в виде так называемого m-файла. Для подготовки, редактирования и отладки m-файлов служит специальный редактор-отладчик, обеспечивающий синтаксический контроль файла.

Текст m-файла, рассчитывающего необходимые для моделирования величины, приводится в Приложении А.

Следует заметить, что пакет MatLab 6.1 не поддерживает кодировку кириллицы что не позволяет использовать русскоязычные комментарии в теле m-файла [16]. В связи с этим комментарии написаны транслитерацией, то есть заменой букв кириллицы созвучными латинскими буквами. В тексте m-файла, приведенного в Приложении А, комментарии для улучшения восприятия заменены русскими.

Кротко поясним назначение основных частей программы:

1. Ввод исходных данных – в память ЭВМ вносятся все необходимые для расчета исходные данные.

2. Промежуточные вычисления – расчет промежуточных величин, которые необходимы для дальнейшего расчета. Расчет тепловых сопротивлений – здесь рассчитываются тепловые сопротивления для ЭТС закрытого обдуваемого двигателя (см. рисунок 2.2).

3. Активные сопротивления обмоток статора и ротора – расчет активных сопротивлений обмоток по формулам (2.99) и (2.102).

4. Расчет потерь – в этой части рассчитываются потери в лобовой и пазовой частях обмотки, необходимые для перехода от схемы (см рисунок 2.2) к схеме (см. рисунок 2.5), а так же константы, необходимые для определения потерь в меди и стали.

5. Расчет коэффициентов теплоотдачи – здесь производится преобразование схемы (см. рисунок 2.2) к схеме (см. рисунок 2.5), определяются тепловые проводимости, вводится замена (2.6) и по выражениям (2.15) – (2.17) определяются коэффициенты А1, А2 и А12.

6. Расчет теплоемкостей – рассчитываются теплоемкости меди и стали по выражениям (2.91) и (2.93).

7. Расчет коэффициентов, учитывающих вклад ротора в нагрев меди и стали – определяются весовые коэффициенты потерь в роторе, входящие в выражения (2.18) и (2.19).

8. Расчет шага интегрирования – здесь определяется оптимальный шаг интегрирования. Это необходимо потому, что используемый по умолчанию метод с переменным шагом не дает желаемого результата и приходится использовать метод с постоянным шагом (в частности метод Рунге-Кутта).

Ниже приводятся исходные данные необходимые для расчета коэффициентов системы дифференциальных уравнений на примере асинхронного двигателя марки 4А132М2У3.

Паспортные данные

3. Номинальная отдаваемая мощность P2=11 кВт;

4. Количество фаз m1=3;

5. Номинальное напряжение U1н=380 В;

6. Синхронная частота вращения n1=3000 об/мин;

7. Количество пар полюсов p=1.

Параметры станины

9. Высота оси вращения h=132 мм;

10. Диаметр станины у основания ребер Dc=0,245 м;

11. Длина свисающей части станины со стороны привода lсв.пр=0,15 м;

12. Длина свисающей части станины со стороны вентилятора lсв.в=0,15 м;

13. Зазор между диффузором и подшипниковым щитом в месте крепления δд.щ=0;

14. Количество ребер станины zp=12;

15. Высота ребра станины hp=23∙10-3 м;