Закон парности касательных напряжений. Главные площадки и главные напряжения

Составим уравнение моментов всех сил, приложенных к элементарному параллелепипеду относительно оси . (рис. 3.1.).

Силы, параллельные этой оси и пересекающие ее, в уравнение не войдут. Моменты сил на двух гранях, перпендикулярных оси , уравновешиваются, равно как и моменты сил png"> на верхней и нижней гранях элемента. Таким образом, получаем:

Отсюда следует, что .

Аналогично из двух других уравнений находим:

Итак, имеем равенства

, (3.1)

называемые законом парности касательных напряжений

Закон парности касательных напряжений – касательные напряжения на двух любых, но взаимно перпендикулярных площадках, направленные перпендикулярно к линии пересечения площадок, равны по величине. При этом они стремятся повернуть элемент в разные стороны.

При изменении ориентации граней выделенного элемента меняются также действующие на его гранях напряжения. Можно провести такие площадки, на которых касательные напряжения равны нулю. Площадки, на которых касательные напряжения равны нулю, называются главными площадками, а нормальные напряжения на этих площадках – главными напряжениями.

Можно доказать, что в каждой точке напряженного тела существует три главные взаимно перпендикулярные площадки.

Главные напряжения обозначают , , . При этом индексы следует расставлять так, чтобы выполнялось неравенство

>>.

Если отличны от нуля все три главных напряжения, то напряженное состояние называется трехосным или объемным.

Если равно нулю одно из главных напряжения, то напряженное состояние называется двухосным или плоским.

Если равно нулю два главных напряжения, то напряженное состояние называется одноосным или линейным.

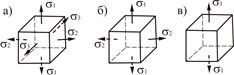
Рис. 3.2