Закон изменения движущих сил, обеспечивающих заданное движение тела. Реакции внешних опор.

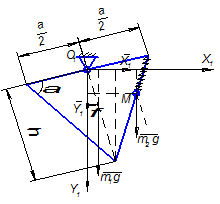
Рис.2 Определение реакций в опорах

Определим проекции реакций опоры на оси неподвижной декартовой системы координат O1x1y1 (рис. 2).

Запишем уравнение теоремы о движении центра масс для рассматриваемой механической системы в векторном виде:

(1.2.1)

Проектируя уравнение (2.1) на оси системы координат О1x1y1 получаем

png">,

(1.2.2)

По известным формулам находим координаты центра тяжести системы,

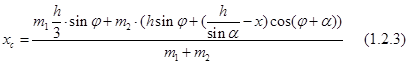
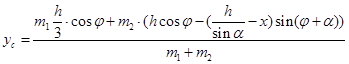(1.2.4)

Дифференцируя уравнения 1.2.3,1.2.4, получим

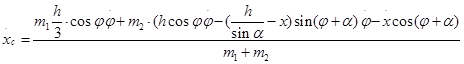
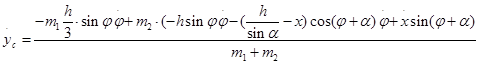
Вычисляя вторые производные получим

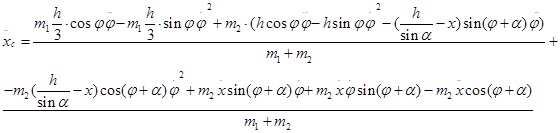
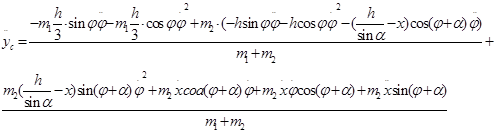(1.2.5)

Подставляя (1.2.5) в уравнения (1.2.2), получаем проекции реакций в опоре О1 на оси неподвижной системы координат:

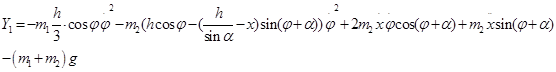
При этом мы учли, что

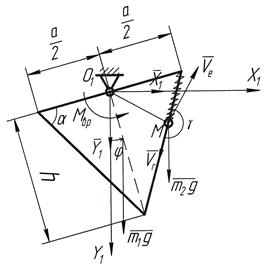
Рис.3 Определение вращательного момента

Применим теорему об изменении кинетического момента для определения внешнего момента, обеспечивающего равномерное движение ведущего звена механической системы. Выберем за ось z ось вращения:

. (1.3.1)

Определим кинетический момент рассматриваемой системы относительно оси Oz.

,

где - осевой момент инерции пластины, -угловая скорость вращения.

Шарик М совершает сложное движение- относительное вдоль желоба пластины(см. рис.3) со скоростью и переносное вместе с пластиной. Переносная скорость перпендикулярна пластине и по модулю равна:

,

где

Кинетический момент шарика относительно оси z равен

,

Кинетический момент всей системы равен

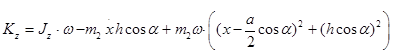(1.3.2)

Определим главный момент внешних сил относительно оси z. Реакции опор пересекают ось вращения и момент относительно этой оси не создают. Определим момент силы тяжести шарика и пластины:

Отсюда имеем:

, (1.3.3)

где Mвр.- внешний момент, обеспечивающий равномерное вращение пластины.

Подставляя 1.3.2, 1.3.3 в уравнение теоремы об изменении кинетического момента системы 1.3.1, получаем

.

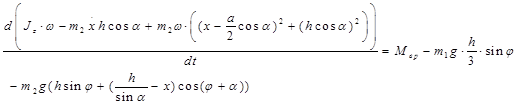Учитывая, что ω=const получим: