Построение физической и математической моделей детектора

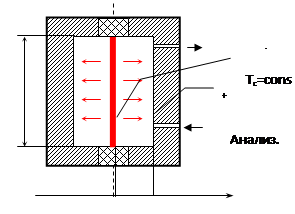
Принцип действия детектора основан на зависимости температуры нагреваемой током проволочки 1 (см. рис.1) от теплопроводности омывающей ее газовой смеси. Подобный детектор (датчик) часто называют катарометр.

Проволочка, натянутая по оси трубки, выполняет одновременно роль нагревателя и термометра сопротивления. С этой целью берется проволока из материала с большим температурным коэффициентом электрического сопротивления, например вольфрама или платины. Если газовая смесь бинарная и теплопроводности компонентов различны, то теплопроводность газовой смеси, а, следовательно, температура и сопротивление нагреваемой током металлической нити зависят от концентрации одного из компонентов смеси.

Температура Тс внутренней поверхности корпуса детектора определяется по результатам измерения температуры ее внешней поверхности с помощью термометра сопротивления или термопар, заделанных в трубку на контролируемом расстоянии.

Метод нагретой нити обычно используется в стационарном варианте. При этом поддерживается постоянной либо мощность, выделяемая в нити, либо температура нити. В нашем случае будем полагать, что электрическая мощность, подводимая к нити, постоянная.

Для того, чтобы получить расчетную формула для температуры нити, примем следующие допущения:

· нить натянута точно по оси трубки;

· перенос тепла излучением и конвекцией отсутствует;

· теплоемкость газа настолько мала, что ею можно пренебречь;

· на внутренней поверхности камеры 2 (см. рисунок 1) поддерживаются граничные условия первого рода.

· торцевые эффекты (т.е. утечка тепла в торцевые части камеры 2 через нить) отсутствуют.

Тогда, математическая модель температурного поля в газовой смеси, омывающей нить запишется в виде:

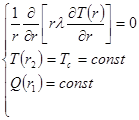
Граничные условия:

1. Температура стенки корпуса – постоянная, т.е

T(r2)=const=Tc .

Такие условия называют граничными условиями первого рода.

2. Тепловой поток на поверхности нити известен и принимается постоянным, т.е.

Q(r1)=const.

Такие граничные условия называют условиями второго рода.

3. Тепловой поток на поверхности нити известен и принимается постоянным, т.е.

Q(r1)=const.

Такие граничные условия называют условиями второго рода.