Построение эпюр и в балках.

Рассмотрим двухопорную балку (рис. 6.5, а). На балку действует в точке сосредоточенный момент , в точке - сосредоточенная сила и на участке - равномерно распределенная нагрузка интенсивностью png">.

Определим опорные реакции и (рис. 6.5, б). Равнодействующая распределенной нагрузки равна , а линия действия ее проходит через центр участка . Составим уравнения моментов относительно точек и .

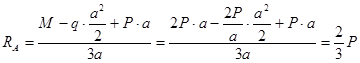
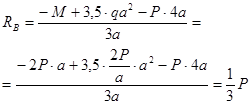
Определим поперечную силу и изгибающий момент в произвольном сечений, расположенном на участке на расстоянии от точки А (рис. 6.5, в). Расстояние может изменяться в пределах ().

Значение поперечной силы не зависит от координаты сечения , следовательно, во всех сечениях участка поперечные силы одинаковы и эпюра имеет вид прямоугольника.

Изгибающий момент изменяется по линейному закону

Для построения эпюры вычисляем ординаты на границах участка.

При :

При

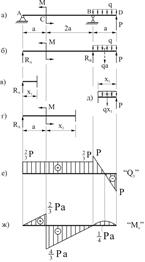
Рис. 6.5

Определим поперечную силу и изгибающий момент в произвольном сечений, расположенном на участке на расстоянии от точки (рис. 6.5, г). Расстояние может изменяться в пределах ().

Значение поперечной силы не зависит от координаты сечения , следовательно, во всех сечениях участка поперечные силы одинаковы и эпюра имеет вид прямоугольника. Изгибающий момент