Определение реакций в опорах методом кинетостатики
Выберем для нашей системы неподвижную систему координат О1X1Y1, (cм. рис.4).
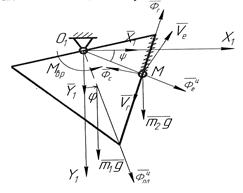
Рис.4. Силы, действующие на систему
Уравнения кинетостатики в векторной форме имеют вид
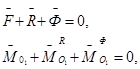
(2.2.1)
где ![]() - главные векторы активных сил, реакций связей и сил инерции;
- главные векторы активных сил, реакций связей и сил инерции;
png">- главные моменты активных сил, реакций связей и сил инерции относительно точки О1.
Сила инерции шарика как материальной точки, совершающей сложное движение, равна геометрической сумме относительной, переносной и кориолисовой сил инерции:
![]()
![]() ,
,
![]()
Сила инерции пластины будет равна:
![]()
Модули сил инерции равны
![]() ,
, ![]() ,
, ![]()
![]() (2.2.2)
(2.2.2)
Изобразим активные силы, реакции опоры и силы инерции, действующие на механическую систему (рис. 4). Векторные уравнения кинетостатики (2.2.1) в проекциях на оси неподвижной системы координат OX1Y1 имеют вид
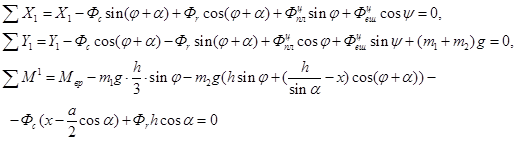 (2.2.3)
(2.2.3)
C учётом выражений для сил инерции (2.2.2), уравнения (2.2.3) принимают вид
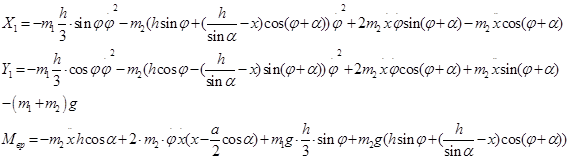
Найденные уравнения реакций шарнира и вращательного момента совпадают с теми, что были найдены в предыдущих частях курсовой работы.
