Кручение прямого круглого бруса.
Точки ![]() и
и ![]() до деформации лежащие на одной образующей, после деформации расположатся на винтовой линии и займут новое положение
до деформации лежащие на одной образующей, после деформации расположатся на винтовой линии и займут новое положение ![]() и
и ![]() .
.
Проведем от точки ![]() прямую
прямую
png">, параллельную
![]() и соединим центр сечения
и соединим центр сечения ![]() с точкой
с точкой ![]() . Тогда угол
. Тогда угол ![]() , равный
, равный ![]() , будет углом поворота сечения
, будет углом поворота сечения ![]() относительно сечения
относительно сечения ![]() . У элемента
. У элемента ![]() до поворота сечения
до поворота сечения ![]() относительно сечения
относительно сечения ![]() верхняя и нижняя стороны были расположены горизонтально. После поворота стороны наклонились и приняли положение
верхняя и нижняя стороны были расположены горизонтально. После поворота стороны наклонились и приняли положение ![]() и
и ![]() . Следовательно, элемент претерпел абсолютный сдвиг, равный длине дуги:
. Следовательно, элемент претерпел абсолютный сдвиг, равный длине дуги:
![]()
Относительный сдвиг будет равен:
![]()
Отношение ![]() представляет относительный угол закручивания
представляет относительный угол закручивания ![]() (угол закручивания на единицу длины бруса). Тогда
(угол закручивания на единицу длины бруса). Тогда
![]() (5.1)
(5.1)
Из этой формулы видно, что относительный сдвиг пропорционален радиусу закручиваемого цилиндрического тела.
На основании закона Гука для сдвига
![]() (5.2)
(5.2)
Можно определить касательное напряжение для элементов лежащих на поверхности вала
![]() (5.3)
(5.3)
Учитывая предположение, что деформация элементов на поверхности вала подобна деформации элементов внутри вала, для произвольного элемента, находящегося на расстоянии ![]() от центра поперечного сечения (рис 5.4)
от центра поперечного сечения (рис 5.4)
![]() (5.4)
(5.4)
![]() (5.5)
(5.5)
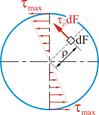
Рис. 5.4
Касательная элементарная сила на площадке ![]() расположенной на расстоянии
расположенной на расстоянии ![]() от оси вала
от оси вала
![]()
Момент элементарной силы относительно оси бруса будет:
![]() (5.6)
(5.6)
Сумма таких элементарных моментов, распространенных по всему поперечному сечению ![]() , при равновесии, наступающем после деформации, должна быть равна крутящему моменту:
, при равновесии, наступающем после деформации, должна быть равна крутящему моменту:
![]() (5.7)
(5.7)
Вынесем постоянные за знак интеграла, получим
![]() (5.8)
(5.8)
Интеграл ![]() является полярным моментом инерции
является полярным моментом инерции ![]() (лекция 2, выражение (2.9)). Тогда
(лекция 2, выражение (2.9)). Тогда
