Кристаллическая структура керамик Tl2Ba2, полученных с использованием высокого давления

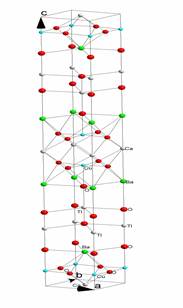
Рис.1 Кристаллическая структура Tl2Ba2CaCu2Oy

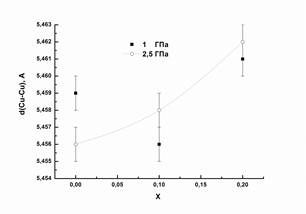
Рис.2 Зависимость расстояния d (Cu - Cu) от содержания фтора (x)

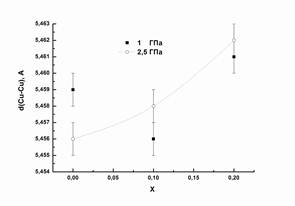
Рис.3 Зависимость температуры перехода в сверхпроводящее состояние от суммы "эффективных" расстояний D1+D2

Таблица 1. Температура перехода в сверхпроводящее состояние образцов системы Tl2Ba2CaCu2O8-x/2Fx (где x=0; 0,1; 0,2)

jpg">

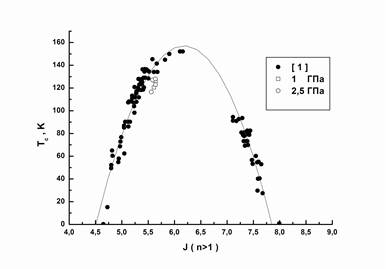
Рис.4. Зависимость температуры перехода в сверхпроводящее состояние от J

Таким образом, возникновение дырок на атомах меди, расположенных на концах диагонали квадрата купратной сетки, должно приводить к следующим структурным изменениям: сжатию квадрата путем смещения атомов меди; сдвигу атомов бария от плоскости квадрата. Сдвиг атомов бария от плоскости квадрата купратной сетки связан с необходимостью сохранения равновесных расстояний между атомами бария и атомами кислорода, расположенными в плоскости CuO2 и соответствует минимальной потенциальной энергии, поэтому он не зависит от способа возникновения дырок. Строя в [1,2,11] зависимость Тс от отношения J (J=d (Cu-Cu) / (D1+D2)) и (D1+D2), авторы обнаружили, что все ВТСП фазы могут быть разделены только на две группы с присущей зависимостью Тс (J): фазы с одним слоем CuO2 и с несколькими слоями. График такой зависимости схож с параболой. Однако, более близкая аппроксимация этой зависимости дает уравнение полинома третьей степени (рис.3,4). J растет с ростом размера и заряда катиона А [2]. Зависимости построены на основе структурных данных 131 соединения (включая Hg-1201, Tl-2201 фазы, имеющие в решетке одну плоскость CuO2, и соединения, имеющие 2-4 плоскости меди, фаз Y-123, 124, 247; Hg-1212, 1213, 1223, 1234, 2212; Tl-1212, 1223, 2212, 2223; Tl0,5Pb0,5-1212,1223; Hg0,5Pb0,5-1212 и др.). На графики нанесены точки, рассчитанные по результатам уточнения наших систем (величины Тс взяты как температуры начала перехода в сверхпроводящее состояние, как и в [1,2,11]). Как может быть видно из графиков, полученные нами точки хорошо "ложатся" на предложенную зависимость. Что с одной стороны подтверждает достаточную точность измерения структурных параметров для образцов нашей системы, а с другой стороны свидетельствует в пользу выбора параметров J и (D1+D2) для описания зависимости температуры перехода в сверхпроводящее состояние от кристаллохимических параметров. Таким образом, управление изменением расстояний Cu-Cu и CuO2 - Ba может явиться одним из способов изменения Тс.

Согласно существующим представлениям, гранулярные ВТСП являются многосвязной джозефсоновской средой [1, 2], в которой имеется сильный пиннинг, поэтому представляется естественным применение концепции критического состояния для описания электродинамики ВТСП. В таких сверхпроводниках существует целый спектр характерных масштабов, приводит к тому, что электродинамика высокотемпературных сверхпроводников оказывается намного более сложной и интересной, нежели обычных. Поэтому исследования в этом направлении имеют как фундаментальное значение для понимания физики многосвязных систем, так и прикладное значение при использовании этих материалов.

Парадигма самоорганизованной критичности (СОК) была сформулирована Баком в 1987 году (см. например [3]). Согласно концепции СОК, гигантские динамические системы, накапливая малые возмущения, естественным образом эволюционируют к критическому состоянию, которое в дальнейшем является самоподдерживающимся, то есть не требует для своего существования точной подстройки внешних параметров. По своей структуре это критическое состояние является набором большого числа метастабильных критических состояний, по которым блуждает система. Очередное малое внешнее воздействие выводит систему из одного метастабильного критического состояния и порождает в ней динамический процесс ("лавину"), по окончании которого система оказывается в другом метастабильном критическом состоянии. Лавины могут быть как малыми, так и гигантскими, охватывающими всю систему, но и те и другие порождаются одинаково малыми возмущениями. Именно такой тип поведения и был назван самоорганизованной критичностью. Находящаяся в самоорганизованном критическом состоянии система теряет характерные масштабы как длины, так и времени, и ее корреляционные функции имеют степенные асимптотики.

Необходимым условием для существования самоорганизации является наличие большого числа близких метастабильных состояний в системе, между которыми происходят переходы. Как было показано в [4], гранулярные сверхпроводники, которые представляют собой джозефсоновскую среду, удовлетворяют этому условию, если количество квантов магнитного потока, запиннингованных на одном элементарном контуре в сверхпроводнике, образованном соседними гранулами, велико. В этом случае континуальное приближение для джозефсоновской среды неприменимо, а гранулярный сверхпроводник необходимо описывать дискретными уравнениями, которые оказываются полностью аналогичными уравнениям для модельной песочной кучи в задаче о самоорганизации. При этом оказалось, что ВАХ сверхпроводника является пространственно изотропной, то есть не зависит от силы Лоренца, что было подтверждено экспериментально в работах [5, 6].