Касательные напряжения при изгибе

Для произвольного сечения (рис. 7.3) величины, входящие в формулу (7.4), имеют следующие значения:

- абсолютная величина поперечной силы в том сечении, где вычисляются касательные напряжения;

- момент инерции этого сечения относительно его нейтральной линии;

- ширина сечения на уровне, где определяют png">;

- абсолютная величина статического момента относительно нейтральной линии той части площади , которая заключена между линией , где определяют , и краем сечения.

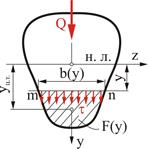
Рис.

7

.

3

Сделаем общие заключения о распределении касательных напряжений в сечении при поперечном изгибе:

1) вид эпюры зависит от формы поперечного сечения балки;

2) в крайних наиболее удаленных от нейтральной линии точках всегда равны нулю;

3) наибольшей величины касательные напряжения для большинства видов сечений достигают на нейтральной линии сечения, причем

, (7.5)

где - - статический момент половины площади сечения.

Формулу (7.5) можно представить в виде

. (7.6)

Здесь - коэффициент, зависящий от формы сечения. Для прямоугольника ; для круглого сечения ;

4) Формулой Журавского можно пользоваться для вычисления касательных напряжений в любых точках массивных профилей.